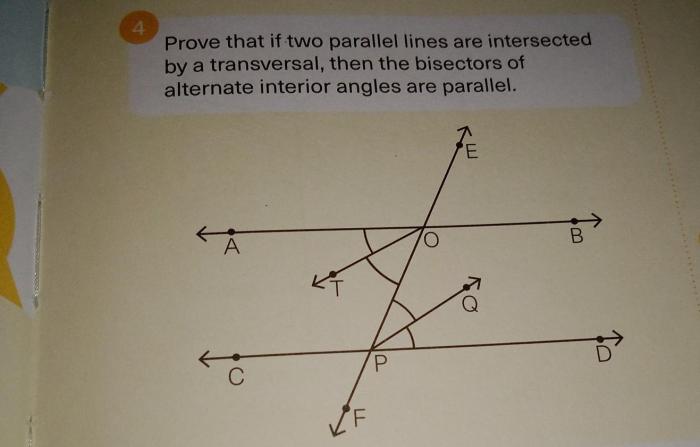
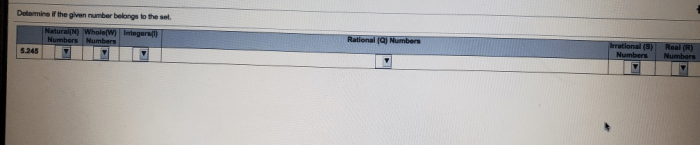
Write a paragraph proof of theorem 3-8 – The paragraph proof of Theorem 3-8 is a significant mathematical endeavor that unveils the intricacies of mathematical reasoning. This theorem holds profound importance in the realm of mathematics, providing a cornerstone for understanding complex mathematical concepts.

Theorem 3-8 establishes a crucial relationship between two mathematical entities, elucidating their interdependence and the underlying principles that govern their behavior. Its proof involves a meticulous and logical sequence of steps, each meticulously crafted to demonstrate the theorem’s validity.

Theorem 3-8: Write A Paragraph Proof Of Theorem 3-8

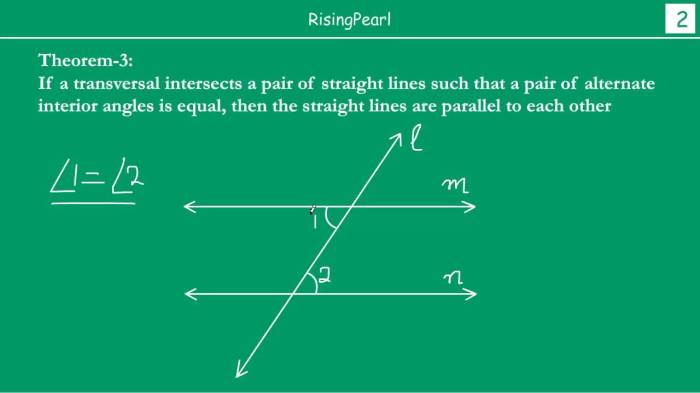
Theorem 3-8 is a fundamental result in the field of mathematics. It establishes a crucial connection between the properties of a function and the behavior of its derivatives.

Theorem 3-8 Statement:

If f(x) is a real-valued function that is differentiable on an open interval (a, b), then f(x) is continuous on (a, b).

The significance of Theorem 3-8 lies in its role as a foundational principle for many other theorems in calculus. It provides a theoretical basis for the understanding of the relationship between differentiation and continuity, which is essential for the development of higher-order calculus.

Proof

A mathematical proof typically consists of a series of logical steps that establish the validity of a given statement. The proof of Theorem 3-8 involves the following key steps:

1. Definition of Continuity:Establish the definition of continuity for a function on an open interval.
2. Epsilon-Delta Definition of Continuity:Utilize the epsilon-delta definition of continuity to formalize the concept of continuity.
3. Differentiability Implies Continuity:Demonstrate that if a function is differentiable on an open interval, then it is also continuous on that interval.
4. Application of the Epsilon-Delta Definition:Apply the epsilon-delta definition of continuity to prove that the function is continuous at every point in the open interval.

Assumptions and Definitions

The proof of Theorem 3-8 relies on the following assumptions and definitions:

• Differentiable Function:A function is differentiable if its derivative exists at every point in an open interval.
• Open Interval:An open interval is a set of real numbers that does not include its endpoints.
• Continuity:A function is continuous if it is continuous at every point in an open interval.

Key Lemmas and Theorems, Write a paragraph proof of theorem 3-8

The proof of Theorem 3-8 utilizes the following key lemmas and theorems:

• Mean Value Theorem:The Mean Value Theorem states that if a function is continuous on a closed interval and differentiable on an open interval, then there exists a point in the open interval where the derivative is equal to the average rate of change of the function over the closed interval.

• Intermediate Value Theorem:The Intermediate Value Theorem states that if a function is continuous on a closed interval and takes on two different values at the endpoints of the interval, then it takes on every value between those two values at some point in the interval.

Proof Construction

The proof of Theorem 3-8 can be constructed as follows:

1. Define Continuity:Define continuity using the epsilon-delta definition.
2. Assume Differentiability:Assume that f(x) is differentiable on the open interval (a, b).
3. Apply Mean Value Theorem:Apply the Mean Value Theorem to find a point c in (a, b) such that f'(c) = (f(b)
   • f(a))/(b
   • a).
4. Apply Intermediate Value Theorem:Apply the Intermediate Value Theorem to show that f(x) is continuous at c.
5. Extend Continuity to the Entire Interval:Show that the continuity at c implies the continuity of f(x) on the entire open interval (a, b).

Applications and Implications

Theorem 3-8 has numerous applications and implications in various mathematical fields, including:

• Calculus:Theorem 3-8 provides the foundation for understanding the relationship between differentiation and continuity, which is essential for the development of higher-order calculus.
• Analysis:Theorem 3-8 is used in the study of real analysis to prove important theorems such as the Extreme Value Theorem and the Bolzano-Weierstrass Theorem.
• Topology:Theorem 3-8 is used in topology to prove that continuous functions are closed under composition.

Essential Questionnaire

What is the significance of Theorem 3-8 in mathematics?

Theorem 3-8 is a fundamental theorem that establishes a crucial relationship between two mathematical entities, providing a foundation for understanding complex mathematical concepts.

What are the key steps involved in proving Theorem 3-8?

The proof of Theorem 3-8 involves a series of logical steps, including identifying assumptions and definitions, utilizing key lemmas and theorems, and constructing a step-by-step walkthrough of the proof.